Pov-ray Cam Cylinder

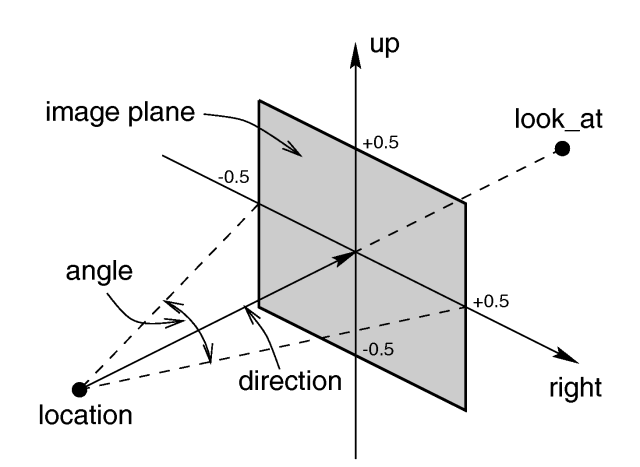
The POV-Ray camera has ten different models, each of which uses a different projection method to project the scene onto your screen. Regardless of the projection type, all cameras use the location, right, up, direction, and keywords to determine the location and orientation of the camera. The type keywords and these four vectors fully define the camera. All other camera modifiers adjust how the camera does its job. The meaning of these vectors and other modifiers differ with the projection type used. A more detailed explanation of the camera types follows later. In the sub-sections which follow, we explain how to place and orient the camera by the use of these four vectors and the sky and look_at modifiers. You may wish to refer to the illustration of the perspective camera below as you read about these.

2.3.1.1 Placing the Camera

2.3.1.1.1 Location and Look_At

Under many circumstances, just two vectors in the camera statement are all you need to position the camera: location and look_at vectors. For example:

camera {

location <3,5,-10>

look_at <0,2,1>

}

The location is simply the x, y, z coordinates of the camera. The camera can be located anywhere in the ray-tracing universe. The default location is <0,0,0>. The look_at vector tells POV-Ray to pan and tilts the camera until it is looking at the specified x, y, z coordinates. By default, the camera looks at a point one unit in the z-direction from the location.

The look_at modifier should almost always be the last item in the camera statement. If other camera items are placed after the look_at vector then the camera may not continue to look at the specified point.

2.3.1.1.2 The Sky Vector

Normally POV-Ray pans left or right by rotating about the y-axis until it lines up with the look_at point and then tilts straight up or down until the point is met exactly. However, you may want to slant the camera sideways like an airplane making a banked turn. You may change the tilt of the camera using the sky vector. For example:

camera {

location <3,5,-10>

sky <1,1,0>

look_at <0,2,1>

}

This tells POV-Ray to roll the camera until the top of the camera is in line with the sky vector. Imagine that the sky vector is an antenna pointing out of the top of the camera. Then it uses the sky vector as the axis of rotation left or right and then tilt up or down in line with the sky until pointing at the look_at point. In effect, you are telling POV-Ray to assume that the sky isn't straight up.

The sky vector does nothing on its own. It only modifies the way the look_at vector turns the camera. The default value is sky<0,1,0>.

2.3.1.1.3 Angles

The angle keyword followed by a float expression specifies the (horizontal) viewing angle in degrees of the camera used. Even though it is possible to use the direction vector to determine the viewing angle for the perspective camera it is much easier to use the angle keyword.

When you specify the angle, POV-Ray adjusts the length of the direction vector accordingly. The formula used is direction_length = 0.5 * right_length / tan(angle / 2) where right_length is the length of the right vector. You should therefore specify the direction and right vectors before the angle keyword. The right vector is explained in the next section.

There is no limitation to the viewing angle except for the perspective projection. If you choose to view angles larger than 360 degrees you will see repeated images of the scene (the way the repetition takes place depends on the camera). This might be useful for special effects.

The spherical camera has the option to also specify a vertical angle. If not specified it defaults to the horizontal angle/2

For example, if you render an image with a 2:1 aspect ratio and map it to a sphere using spherical mapping, it will recreate the scene. Another use is to map it onto an object and if you specify transformations for the object before the texture, say in an animation, it will look like reflections of the environment (sometimes called environment mapping).

2.3.1.1.4 The Direction Vector

You will probably not need to explicitly specify or change the camera direction vector but it is described here in case you do. It tells POV-Ray the initial direction to point the camera before moving it with the look_at or rotate vectors (the default value is direction<0,0,1>). It may also be used to control the (horizontal) field of view with some types of projection. The length of the vector determines the distance of the viewing plane from the camera's location. A shorter direction vector gives a wider view while a longer vector zooms in for close-ups. In early versions of POV-Ray, this was the only way to adjust the field of view. However, zooming should now be done using the easier-to-use angle keyword.

If you are using the ultra_wide_angle, panoramic, or cylindrical projection you should use a unit length direction vector to avoid strange results. The length of the direction vector does not matter when using the orthographic, fisheye, or omnimax projection types.

2.3.1.1.5 Up and Right Vectors

The primary purpose of the up and right vectors is to tell POV-Ray the relative height and width of the view screen. The default values are:

right 4/3*x

up y

In the default perspective camera, these two vectors also define the initial plane of the view screen before moving it with the look_at or rotate vectors. The length of the right vector (together with the direction vector) may also be used to control the (horizontal) field of view with some types of projection. The look_at modifier changes both the up and right vectors. The angle calculation depends on the right vector.

Most camera types treat the up and right vectors the same as the perspective type. However several make special use of them. In the orthographic projection: The lengths of the up and right vectors set the size of the viewing window regardless of the direction vector length, which is not used by the orthographic camera.

When using cylindrical projection: types 1 and 3, the axis of the cylinder lies along the up vector and the width is determined by the length of the right vector or it may be overridden with the angle vector. In type 3 the up vector determines how many units high the image is. For example, if you have up 4*yon a camera at the origin. Only points from y=2 to y=-2 are visible. All viewing rays are perpendicular to the y-axis. For types 2 and 4, the cylinder lies along the right vector. Viewing rays for type 4 are perpendicular to the right vector.

Note: that the up, right, and direction vectors should always remain perpendicular to each other or the image will be distorted. If this is not the case a warning message will be printed. The vista buffer will not work for non-perpendicular camera vectors.

2.3.1.1.6 Aspect Ratio

Together the up and right vectors define the aspect ratio (height to width ratio) of the resulting image. The default values up<0,1,0> and right<1.33,0,0> result in an aspect ratio of 4 to 3. This is the aspect ratio of a typical computer monitor. If you wanted a tall skinny image or a short wide panoramic image or a perfectly square image you should adjust the up and right vectors to the appropriate proportions.

Most computer video modes and graphics printers use perfectly square pixels. For example, Macintosh displays and IBM SVGA modes 640x480, 800x600, and 1024x768 all use square pixels. When your intended viewing method uses square pixels then the width and height you set with the Width and Height options or +W or +H switches should also have the same ratio as the up and right vectors.

Note: 640/480 = 4/3 so the ratio is proper for this square pixel mode.

Not all display modes use square pixels, however. For example, IBM VGA mode 320x200 and Amiga 320x400 modes do not use square pixels. These two modes still produce a 4/3 aspect ratio image. Therefore images intended to be viewed on such hardware should still use a 4/3 ratio on their up and right vectors but the pixel settings will not be 4/3.

For example:

camera {

location <3,5,-10>

up <0,1,0>

right <1,0,0>

look_at <0,2,1>

}

This specifies a perfectly square image. On a square pixel display like SVGA, you would use pixel settings such as +W480 +H480 or +W600 +H600. However on the non-square pixel Amiga 320x400 mode you would want to use values of +W240 +H400 to render a square image.

The bottom line issue is this: the up and right vectors should specify the artist's intended aspect ratio for the image and the pixel settings should be adjusted to that same ratio for square pixels and to an adjusted pixel resolution for non-square pixels. The up and right vectors should not be adjusted based on non-square pixels.

2.3.1.1.7 Handedness

The right vector also describes the direction to the right of the camera. It tells POV-Ray where the right side of your screen is. The sign of the right vector can be used to determine the handedness of the coordinate system in use. The default value is: right<1.33,0,0>. This means that the +x-direction is to the right. It is called a left-handed system because you can use your left hand to keep track of the axes. Hold out your left hand with your palm facing to your right. Stick your thumb up. Point straight ahead with your index finger. Point your other fingers to the right. Your bent fingers are pointing to the +x-direction. Your thumb now points into +y-direction. Your index finger points into the +z-direction.

To use a right-handed coordinate system, as is popular in some CAD programs and other ray-tracers, make the same shape using your right hand. Your thumb still points up in the +y-direction and your index finger still points forward in the +z-direction but your other fingers now say the +x-direction is to the left. That means that the right side of your screen is now in the -x-direction. To tell POV-Ray to act like this you can use a negative x value in the right vector such as right<-1.33,0,0>. Since having x values increasing to the left does not make much sense on a 2D screen you now rotate the whole thing 180 degrees around by using a positive z value in your camera's location. You end up with something like this.

camera {

location <0,0,10>

up <0,1,0>

right <-1.33,0,0>

look_at <0,0,0>

}

Now when you do your raytracer's aerobics, as explained in the section "Understanding POV-Ray's Coordinate System", you use your right hand to determine the direction of rotations.

In a two-dimensional grid, x is always to the right and y is up. The two versions of handedness arise from the question of whether z points into the screen or out of it and which axis in your computer model relates to up in the real world.

Architectural CAD systems, like AutoCAD, tend to use the God's Eye orientation that the z-axis is the elevation and is the model's up direction. This approach makes sense if you are an architect looking at a building blueprint on a computer screen. z means up, and it increases towards you, with x and y still across and up the screen. This is the basic right-handed system.

Stand-alone rendering systems, like POV-Ray, tend to consider you as a participant. You are looking at the screen as if you were a photographer standing in the scene. The up direction in the model is now y, the same as up in the real world, and x is still to the right, so z must be depth, which increases away from you into the screen. This is the basic left-handed system.

2.3.1.1.8 Transforming the Camera

The various transformations such as translate and rotate modifiers can re-position the camera once you have defined it. For example:

camera {

location < 0, 0, 0>

direction < 0, 0, 1>

up < 0, 1, 0>

right < 1, 0, 0>

rotate <30, 60, 30>

translate < 5, 3, 4>

}

In this example, the camera is created, then rotated by 30 degrees about the x-axis, 60 degrees about the y-axis, and 30 degrees about the z-axis, then translated to another point in space.